miloR的学习与使用

miloR R包的使用

miloR Learning

1. 背景

John C. Marioni 教授是国际知名的计算生物学家，在位于英国剑桥希克斯顿（Hinxton）的惠康基因组研究园（Wellcome Genome Campus）长期担任重要领导职务。他的研究开创了单细胞基因组学数据分析的统计方法，对转录组学领域产生了深远影响。

miloR 在《Nature Biotechnology》是由John C. Marioni发表，Differential abundance testing on single-cell data using k-nearest neighbor graphs

R包 的链接 (https://github.com/MarioniLab/miloR)

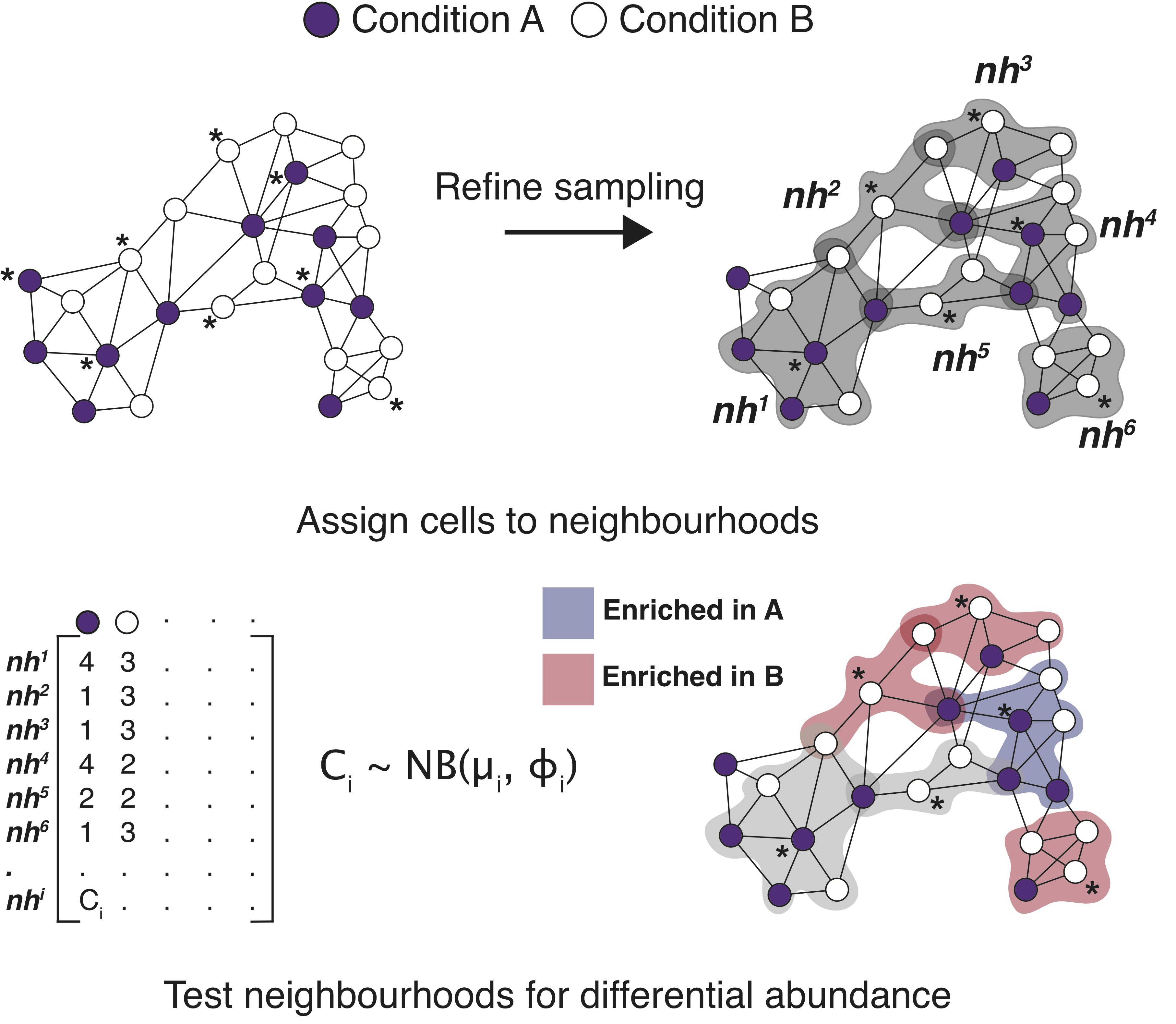
miloR

Milo 分析流程示意图

为了解决这些挑战，Marioni开发了一种计算框架，可以在不依赖将细胞聚类成离散组的情况下进行差异丰度测试。利用了一种常见于许多单细胞分析中的数据结构：k近邻（KNN）图。我们将细胞状态建模为该图上的重叠邻域，并将其作为差异丰度检验的基础。为了解决重叠邻域之间的非独立性问题，应用了加权版的Benjamini-Hochberg方法，其中P值由邻域连通性的倒数加权——这是对先前描述的用于控制空间错误发现率（FDR）策略的一种图式改进。

Note

Milo 的方法利用了广义线性模型 (GLM) 的灵活性，从而可以进行复杂的实验设计，例如纳入干扰和技术协变量，包括考虑从不同批次中确定的样本。

1.1 关键步骤

  1. 构建KNN图

基于降维后的细胞嵌入（如 PCA、UMAP），计算细胞间的欧氏距离，构建 K-最近邻图（KNN graph）。 每个细胞的邻域定义为与其最近的 k 个邻居（默认 k=30），形成重叠的局部细胞群体。

Milo 使用基于基因表达空间相似性计算的 KNN 图来表示细胞所在的表型流形。为了构建 KNN 图，我们遵循单细胞分析的最佳实践40，通过按每个细胞的测序深度重新缩放唯一分子标识符计数，应用对数变换，并将 M 个细胞的基因表达矩阵投影到 d 个主要主成分 (PC) 上。

原始数据中，每个细胞都有两万多个基因(维度)

    1. 降维后的细胞嵌入，把细胞放进坐标系
    • PCA/UMAP的作用：将每个细胞简化为低维度空间中的一个点
    • 空间含义：靠近的点表示转录组特征相似
    1. 构建KNN图：建立邻里关系
    • KNN (K-Nearest Neighbors) 的核心是为每一个细胞找“邻居”
    • 欧氏距离：算法计算一个细胞到其他所有细胞的直线距离
    • 连线：对于细胞A，算法选出距离它最近的k个细胞(默认是30)，并在它们之间连上一条线
    • 结果：所有细胞和这些连线构成了一个巨大的社交网络，功能相似的细胞被紧密的锁在一个圈子里
  1. 定义领域(Neighborhoods)

对每个细胞，统计其所属的邻域（即作为其他细胞的邻居的次数），形成邻域-细胞矩阵。 通过 图抽样（graph sampling） 减少冗余，保留代表性邻域。

  1. Counting cells in neighborhoods

对于每个邻域，我们统计每个实验样本 S 中的细胞数量，构建一个 N × S（邻域 × 实验样本计数）矩阵。

  1. Testing for differential abundance in neighborhoods

对每个邻域中存在的细胞数量进行计数（每个实验样品），并将其用于条件之间的差异丰度测试。

为了检验差异丰度，我们使用 edgeR 中的 QL 方法分析邻域计数，类似于 Cydar 中的实现方式。

Tip

准似然检验（Quasi-Likelihood, QL）

QL 方法的优势在于它不仅估计了基因（或邻域）层面的离散度，还通过 QL 分散度（QL dispersion） 捕捉了数据中的不确定性，这比传统的似然比检验（Likelihood Ratio Test）更能有效地控制假阳性率（FDR）

我们对每个邻域的计数拟合一个负二项广义线性模型（NB GLM），并使用 TMM 归一化来考虑不同样本中细胞数量的差异,使用指定对比的 QL F 检验来计算每个邻域的 P 值。

  1. Controlling the spatial FDR in neighborhoods

使用 FDR（如 Benjamini-Hochberg）校正邻域水平的 p 值，控制假阳性率。

空间 FDR 可以解释为邻域并集中被假阳性邻域所占的比例。为了控制 KNN 图中的空间 FDR，我们应用了 Benjamini-Hochberg 方法的加权版本，其中 P 值由邻域连通性的倒数加权。作为邻域连通性的衡量标准，我们使用每个邻域中索引单元格到第 k 个最近邻的欧氏距离。

  1. 可视化

为了可视化邻域差异分析的结果，我们构建了一个抽象图，其中节点代表邻域，边代表邻域间共有的细胞数量。节点的大小代表邻域内的细胞数量。节点的位置由采样索引细胞在单细胞均匀流形近似和投影（UMAP）中的位置决定，以便与单细胞嵌入进行定性比较。图形可视化使用 R 包 ggplot 和 ggraph 实现。

2. miloR Tutorials

# install
BiocManager::install("miloR")

# library
library(miloR)
library(SingleCellExperiment)
library(scater)
library(scran)
library(dplyr)
library(patchwork)

2.1 Basic Milo 模拟数据

  1. 加载数据

使用miloR自带的数据集，traj_sce 是大的SingleCellExperiment数据类型

Tip

之前已经介绍过 seurat ，是当前最常用的单细胞转录组分析工具，主要是从原始数据到聚类注释再到可视化，是一个高度封装、一站式解决方案，但是seurat背后的数据结构–SingleCellExperiment（SCE）

SingleCellExperiment 是 Bioconductor 项目设计的基础类，继承自 SummarizedExperiment，专为单细胞数据存储与分析而优化。SCE 可以统一存储表达矩阵、细胞/基因元数据、降维结果等信息，并被上百个 Bioconductor 单细胞工具所支持。通过 Seurat v5 中的 as.SingleCellExperiment() 与 as.Seurat() 函数，可以在两个体系之间自由转换。

“想象 SCE 对象是一艘货轮，每个 slot 就是一个专用货箱，分别存储不同类型的数据，整船出发就是一次完整的数据分析旅程

data("sim_trajectory", package = "miloR")

## Extract SingleCellExperiment object
traj_sce <- sim_trajectory[['SCE']]

## Extract sample metadata to use for testing
traj_meta <- sim_trajectory[["meta"]]

## Add metadata to colData slot
colData(traj_sce) <- DataFrame(traj_meta)
colnames(traj_sce) <- colData(traj_sce)$cell_id

redim <- reducedDim(traj_sce, "PCA")
dimnames(redim) <- list(colnames(traj_sce), paste0("PC", c(1:50)))
reducedDim(traj_sce, "PCA") <- redim

看完SingleCellExperiment 之后，就能了解到数据集中数据的组成和含义了

> traj_sce
class: SingleCellExperiment 
dim: 500 500 
metadata(0):
assays(2): counts logcounts
rownames(500): G1 G2 ... G499 G500
rowData names(0):
colnames(500): C1 C2 ... C499 C500
colData names(2): cell_id group_id
reducedDimNames(1): PCA
mainExpName: NULL
altExpNames(0):
  • rowData 表示基因信息
  • colData 表示细胞信息
  • assays 表示count信息
  • reducedDimNames 表示降维信息
  1. Pre-processing

对于DA分析，需要构建单细胞的无向KNN图,标准的单细胞分析流程通常基于PCA中的距离来实现这一点,使用scater进行归一化并计算主成分还可以运行UMAP进行可视化

logcounts(traj_sce) <- log(counts(traj_sce)+1)
traj_sce <- runPCA(traj_sce, ncomponents = 30)
traj_sce <- runUMAP(traj_sce)

plotUMAP(traj_sce)
  1. Create a Milo object

用不同来源的数据，构建Milo数据结构，核心还是获取到细胞基因的表达矩阵

(1). From SingleCellExperiment object

为了对图邻域进行差异丰度分析，首先构建一个 Milo 对象。该对象扩展了 SingleCellExperiment 类，用于存储 KNN 图上邻域的信息。

# 3. create milo
traj_milo <- Milo(traj_sce)
reducedDim(traj_milo, "UMAP") <- reducedDim(traj_sce, "UMAP")

Milo是SCE的延续，增加了新的slot用来记录后续的数据

> traj_milo
class: Milo 
dim: 500 500 
metadata(0):
assays(2): counts logcounts
rownames(500): G1 G2 ... G499 G500
rowData names(0):
colnames(500): C1 C2 ... C499 C500
colData names(5): cell_id group_id Condition Replicate Sample
reducedDimNames(2): PCA UMAP
mainExpName: NULL
altExpNames(0):
nhoods dimensions(2): 1 1
nhoodCounts dimensions(2): 1 1
nhoodDistances dimension(1): 0
graph names(0):
nhoodIndex names(1): 0
nhoodExpression dimension(2): 1 1
nhoodReducedDim names(0):
nhoodGraph names(0):
nhoodAdjacency dimension(2): 1 1

  • nhoods:这是最关键的矩阵。它记录了哪些细胞属于哪个邻域

    • 通常是一个二元矩阵（0 或 1），行代表细胞，列代表邻域中心。

  • nhoodIndex:存储了作为每个邻域“圆心”（Index cells）的细胞索引。Milo 并不会在每个细胞周围都建邻域，而是挑选一部分具有代表性的细胞作为中心

  • nhoodCounts: 邻域丰度矩阵

    • 行是邻域，列是样本
    • 微分丰度（Differential Abundance）分析的基础数据
    • nhoodExpression: 记录了每个邻域中基因的平均表达水平。这对于后续分析“哪个邻域对应哪种细胞特征”非常有用

  • nhoodDistances: 记录了邻域中心细胞之间的距离

  • nhoodAdjacency: 邻域的邻接矩阵，记录了哪些邻域之间是有重叠或相邻关系的

  • nhoodGraph/graph: 存储了基于邻域构建的图结构

(2). From AnnData object (.h5ad)

可以使用 zellkonverter 包，从存储为 h5ad 文件的 AnnData 对象创建一个 SingleCellExperiment 对象。

library(zellkonverter)

# Obtaining an example H5AD file.
example_h5ad <- system.file("extdata", "krumsiek11.h5ad",
                            package = "zellkonverter")

example_h5ad_sce <- readH5AD(example_h5ad)
example_h5ad_milo <- Milo(example_h5ad_sce)

(3). From Seurat object

从Seurat转换也是常见的方法，但是必须是SingleCellExperiment

library(Seurat)
data("pbmc_small")
pbmc_small_sce <- as.SingleCellExperiment(pbmc_small)
pbmc_small_milo <- Milo(pbmc_small_sce)
  1. Construct KNN graph

将 KNN 图添加到 Milo 对象中。该图以 igraph 格式存储在 graph 插槽中。miloR 包包含从存储在 reducedDim 插槽中的 PCA 维度构建和存储该图的功能

traj_milo <- buildGraph(traj_milo, k = 10, d = 30)

结果是一个复杂的igraph对象，其核心数据结构主要由两部分组成

  • 节点(Vetices):数量等于数据中细胞总数，每个节点都有唯一的ID
  • 边(Edges): AB连成一条线
> traj_milo@graph
$graph
IGRAPH 3d3d461 U--- 500 3920 -- 
+ edges from 3d3d461:
 [1] 1--  4 1-- 11 1-- 18 1-- 38 1-- 78 1-- 92 1--155 1--164 1--184 1--194 1--195 1--243 1--260 1--274
 [15] 1--280 1--358 1--392 1--405 1--436 1--456 1--486 1--499 2-- 95 2--187 2--198 2--202 2--226 2--233
 [29] 2--322 2--393 2--478 2--482 3--  5 3-- 20 3-- 43 3-- 57 3--153 3--290 3--299 3--300 3--333 3--491
 [43] 4-- 92 4-- 99 4--214 4--270 4--298 4--304 4--328 4--358 4--366 4--401 4--468 4--469 5-- 20 5-- 24
 [57] 5-- 43 5-- 49 5-- 51 5-- 54 5-- 57 5-- 75 5-- 86 5-- 88 5--108 5--112 5--133 5--162 5--204 5--215
 [71] 5--254 5--259 5--290 5--296 5--299 5--318 5--333 5--367 5--395 5--407 5--451 5--466 5--474 5--491
 [85] 6-- 80 6--115 6--136 6--143 6--199 6--204 6--263 6--269 6--275 6--286 6--318 6--330 6--333 6--466
 [99] 7-- 28 7-- 56 7--104 7--111 7--134 7--285 7--398 7--416 7--435 7--465 8-- 17 8-- 40 8-- 78 8-- 92
[113] 8-- 98 8--104 8--134 8--155 8--288 8--304 8--366 8--416 8--469 9-- 27 9-- 44 9-- 46 9-- 51 9-- 54
+ ... omitted several edges
  • IGRAPH UN– [节点数] [边数] –
  • UN (Undirected, Unweighted)
  1. 界定代表性neighbourhoods

上一步中将单元格的邻域（索引）定义为 KNN 图中与索引单元格通过边连接的单元格组。不测试每个细胞邻域内的 DA，对代表性细胞子集进行采样作为索引

  • prop:随机抽样的初始细胞比例（通常 0.1 - 0.2 就足够了）
  • k: 用于 KNN 细化的 k 值（建议使用与 KNN 图构建相同的 k 值）
  • d: 用于 KNN 细化的降维维度数量（建议使用与 KNN 图构建相同的 d 值）
  • refined 指明是否要使用采样细化算法，或者只是随机选择单元格,默认且推荐的方法是使用优化算法。只有当您使用基于图的校正算法（例如 BBKNN）对数据进行批量校正后，DA 测试结果仍不理想时，才可以考虑使用随机算法

定义好邻域之后，最好查看一下邻域的大小（即每个邻域包含多少个单元格）。这会影响DA测试的效力。

traj_milo <- makeNhoods(traj_milo, prop = 0.1, k = 10, d=30, refined = TRUE)

plotNhoodSizeHist(traj_milo)

dgCMatrix类，d：代表 double。表示矩阵中存储的是双精度浮点数（实数）；g：代表 general。表示这是一个一般的矩阵，没有特殊的对称性或三角结构；C代表 column-compressed。表示它是按列压缩存储的。

traj_milo@nhoods

  • 行（Rows）：代表所有的细胞（与原始输入数据中的细胞一一对应）
  • 列（Columns）：代表被选为邻域中心的索引细胞（Index Cells）
  • 数值：
    • 1: 表示该行对应的细胞属于该列对应的邻域
    • 0: 表示该行对应的细胞不属于该邻域
  1. 计算邻域cells

需要统计每个样本中每个邻域内的细胞数量，需要使用细胞元数据，并指定哪一列包含样本信息。

traj_milo <- countCells(traj_milo, meta.data = data.frame(colData(traj_milo)), samples="Sample")

这会在 Milo 对象中添加一个 n × m 矩阵，其中 n 是邻域的数量，m 是实验样本的数量。 m 的值表示每个样本在每个邻域中计数的细胞数量。该计数矩阵将用于 DA 测试。

Note

colData是要取细胞对应的信息包括细胞信息，样本信息，分组信息，疾病信息等

核心是输入样本信息的列

  1. Differential abundance testing

广义线性模型 (GLM) 框架中实现了这一假设检验,主要是edgeR中的Negative Binomial GLM

首先需要考虑实验设计。设计矩阵应该将样本与感兴趣的条件相匹配。在本例中，条件就是我们要检验的协变量。

traj_design <- data.frame(colData(traj_milo))[,c("Sample","Condition")]
traj_design <- distinct(traj_design)
rownames(traj_design)<- traj_design$Sample

traj_design <- traj_design[colnames(nhoodCounts(traj_milo)), , drop=FALSE]

Milo 采用了 cydar 引入的空间 FDR 校正的改进版本，该版本考虑了邻域之间的重叠。具体来说，每个假设检验的 P 值都按第 k 个最近邻距离的倒数进行加权。要使用此统计数据，首先需要将最近邻居之间的距离存储在 Milo 对象中。

traj_milo <- calcNhoodDistance(traj_milo, d=30)

rownames(traj_design) <- traj_design$Sample
da_results <- testNhoods(traj_milo, design = ~ Condition, design.df = traj_design)
  1. 可视化 为了可视化 DA 结果，我们构建了一个抽象的邻域图，我们可以将其叠加到单细胞嵌入上
plotUMAP(traj_milo) + plotNhoodGraphDA(traj_milo, da_results, alpha=0.05) +
  plot_layout(guides="collect")

2.2 利用 Milo 进行差异丰度检验——小鼠原肠胚形成示例

For this vignette we will use the mouse gastrulation single-cell data from Pijuan-Sala et al. 2019. The dataset can be downloaded as a SingleCellExperiment object from the MouseGastrulationData package on Bioconductor. To make computations faster, here we will download just a subset of samples, 4 samples at stage E7 and 4 samples at stage E7.5.

该数据集已经过预处理，并包含一个经过 pca 校正的降维，该降维是在使用 fastMNN 进行批量校正后构建的

# 0. Load packages
library(miloR)
library(SingleCellExperiment)
library(scater)
library(scran)
library(dplyr)
library(patchwork)
library(MouseGastrulationData)

# 1. Loda data
select_samples <- c(2,  3,  6, 15,
                    # 4, 19, 
                    10, 14, 20, 30
                    #31, 32
                    )
embryo_data = EmbryoAtlasData(samples = select_samples)

# 2. Visualize the data
embryo_data <- embryo_data[,apply(reducedDim(embryo_data, "pca.corrected"), 1, function(x) !all(is.na(x)))]
embryo_data <- runUMAP(embryo_data, dimred = "pca.corrected", name = 'umap')

plotReducedDim(embryo_data, colour_by="stage", dimred = "umap") 

# 3. DA testing
## 3.1 Create a milo object
embryo_milo <- Milo(embryo_data) %>%
    buildGraph(embryo_milo, k = 30, d = 30, reduced.dim = "pca.corrected")%>%
    makeNhoods(embryo_milo, prop = 0.1, k = 30, d=30, refined = TRUE, reduced_dims = "pca.corrected")
## 3.2 average neighbourhood size over 5 x N_samples.
plotNhoodSizeHist(embryo_milo)

## 3.3 Counting cells in neighbourhoods
embryo_milo <- countCells(embryo_milo, meta.data = as.data.frame(colData(embryo_milo)), sample="sample")

## 3.4 Defining experimental design
embryo_design <- data.frame(colData(embryo_milo))[,c("sample", "stage", "sequencing.batch")]
embryo_design$sequencing.batch <- as.factor(embryo_design$sequencing.batch) 
embryo_design <- distinct(embryo_design)
rownames(embryo_design) <- embryo_design$sample

## 3.5 Computing neighbourhood connectivity
embryo_milo <- calcNhoodDistance(embryo_milo, d=30, reduced.dim = "pca.corrected")

## 3.6 Testing
da_results <- testNhoods(embryo_milo, design = ~ sequencing.batch + stage, design.df = embryo_design)

## 3.7 Inspecting DA testing results
ggplot(da_results, aes(PValue)) + geom_histogram(bins=50)

ggplot(da_results, aes(logFC, -log10(SpatialFDR))) + 
  geom_point() +
  geom_hline(yintercept = 1) ## Mark significance threshold (10% FDR)

embryo_milo <- buildNhoodGraph(embryo_milo)

### Plot single-cell UMAP
umap_pl <- plotReducedDim(embryo_milo, dimred = "umap", colour_by="stage", text_by = "celltype", 
                          text_size = 3, point_size=0.5) +
  guides(fill="none")

### Plot neighbourhood graph
nh_graph_pl <- plotNhoodGraphDA(embryo_milo, da_results, layout="umap",alpha=0.1) 
  
umap_pl + nh_graph_pl +
  plot_layout(guides="collect")

plotDAbeeswarm(da_results, group.by = "celltype")
Note

  • 不健康的分布（\(k\) 太小）：直方图在左侧（接近 0 的地方）有一个很高的峰。这说明你的邻域太“碎”了，每个邻域包含的细胞不足以支撑后续的统计检验。

  • 不健康的分布（\(k\) 太大）：虽然统计效力提高了，但邻域会变得过于庞大，导致不同细胞类型的特征被混在一起，失去了空间分辨率（即你无法区分到底是哪种微小的细胞状态发生了变化）。